مقایسه میانگین یک متغیر پنهان در بین دو یا چند گروه
هدف از نگارش این متن معرفی روشی است که بر مبنای آن می توان به مقایسه میانگین یک متغیر پنهان فاصله ای یا نسبی در بین دو یا چند گروه دست زد. تحلیل ساختارهای میانگین بر آزمون فرضیه هایی متمرکز است که درباره میانگین متغیرهای پنهان صورت بندی می شود.
به عبارت دیگر تحلیل ساختارهای میانگین را می توان به عنوان روشی قلمداد کرد که به هنگام طرح فرضیه درباره میانگین یک یا چند متغیر پنهان جایگزینی برای آزمون T یا F است. آزمون هایی که با متغیرهای پنهان در نقش متغیر مشاهده شده رفتار می کنند.
موضوع تحلیل ساختارهای میانگین
در مطالعات اجتماعی مدل های تحلیل شده معمولا از نوع مدل های عاملی تأییدی در نقش مدل های اندازه گیری، مدل های مسیر با متغیرهای شاهده شده به منظور تبیین متغیرهای وابسته مشاهده شده و مدل های معادله ساختاری برای تبیین متغیرهای وابسته پنهان است. در هیچ یک از انواع مدل های ذکر شده به طور معمول، میانگین ها تحلیل نمی شوند.
داده های ورودی در شکل ماتریس کواریانس و اطلاعات خروجی نیز در قالب برآورد واریانس ها، کواریانس ها و وزن های رگرسیونی برای جامعه آماری می باشد. این در حالی است که تحلیل ساختارهای میانگین برای سازه های پنهان کمتر مورد توجه پژوهشگران بوده است هرچند این نوع از تحلیل می تواند کاربرد بسیاری برای مقایسه میانگین این نوع از متغیرها در مطالعات علمی بخصوص مطالعات علوم اجتماعی داشته باشد.
روش هایی نظیر تحلیل واریانس هرچند به برآورد و مقایسه میانگین ها می پرازد اما از این نقطه ضعف درونی رنج می برد که با متغیرهای آزمون به عنوان متغیر مشاهده شده رفتار می کند، هرچند این متغیرها در واقع سازه هایی پنهان باشند. در چنین وضعیتی، نمرات آزمودنی ها برای سازه های پنهانی که به عنوان متغیر مشاهده شده در نظر گرفته شده اند دارای دقت کامل فرض می شوند، هرچند ضرایبی نظیر آلفای کرونباخ، اسپیرمن- براون و کودر ریچاردسون که برای برآورد دقت اندازه گیری یا نسبت واریانس واقعی به واریانس کل طرح شده اند، چنین فرضیه ای را تأیید نکنند.
مثال
به عنوان مثال فرض کنید محققی مایل است که به مقایسه آگاهی دو گروه زنان و مردان از حقوق شهروندی در یک جامعه آماری دست زند. آگاهی از حقوق شهروندان سازه ای پنهانی است که به هنگام اندازه گیری نمرات هریک از واحدهای نمونه انتظار داریم آنچه اندازه گیری می شود به طور کامل منعکس کننده آگای از حقوق شهروندی نباشد بلکه عوامل دیگری باعث شوند تا دقت اندازه گیری صد در صد نباشد.
بنابراین استفاده از نمرات افراد مورد مطالعه در یک تحلیل واریانس برای مقایسه میانگین های زنان و مردان در حالیکه دقت اندازه گیری کامل نیست (ولی کامل فرض می شود) می تواند به نتایج با دقت پایین و احتمالا اشتباه بیانجامد. به عبارتی تفاوت میانگین ها معنا دار تلقی شود در حالیکه این تفاوت در واقع نشئت گرفته از خطای اندازه گیری است، خطایی که هنگام آزمون فرضیه نادیده گرفته شده است.
تحلیل ساختارهای میانگین روشی است که با سازه های پنهان که فاقد دقت اندازه گیری صد در صد ولی قابل قبول هستند در عمل به عنوان سازه های نهان دارای خطای اندازه گیری (و نه متغیرهای مشاهده شده فاقد خطای اندازه گیری) برخورد می کند و بنابراین تلاش می کند از نقطه ضعف روش هایی نظیر تحلیل واریانس دور شود.
پیش فرض های تحلیل ساختارهای میانگین
تحلیل ساختارهای میانگین برای بررسی تفاوت بین میانگین دو یا چند سازه پنهان در بین دو یا چند گروه حداقل نیازمند برقرار بودن دو پیش فرض است که بررسی هر دو پیش فرض با استفاده از تحلیل ساختارهای کواریانس انجام می شود. این دو پیش فرض عبارتند از :
- مدل اندازه گیری بر مبنای تحلیل ساختارهای کواریانس به لحاظ علمی قابل قبول باشد. قابل بودن آن به لحاظ علمی منوط به دارا بودن شاخص های برازش تطبیقی و شاخص های برازش مقتصد برابر یا بزرگتر از مقادیر قابل قبول است. همچنین مقدار آماره کای دو نسبی و مطلق و شاخص ریشه دوم میانگین مربعات خطای برآورد از جمله دیگر شاخص های مورد استفاده هستند. چنین پیش فرضی براساس این منطق است که اگر مدل اندازه گیری برای سنجش سازه پنهان قابل قبول نیست بنابراین مقایسه میانگین ها برای آن سازه در بین دو یا چند گروه بر مبنای آن مدل بی معناست. این پیش فرض به طور ضمنی عنوان می کند که در صورت پایین بودن شاخص های نیکویی برازش ضرورت دارد تا با اصلاح مدل اندازه گیری به یک مدل قابل قبول دست یابیم.
- ضرورت دارد اجزای مدل اندازه گیری در بین نمونه های مورد مقایسه معادل یا یکسان باشند.
مدل های عاملی تأییدی با شاخص های برازش قابل قبول
شوماخر و لومکس در بحث خود درباره مدل میانگین های ساختمند، بر قابل قبول بودن شاخص های برازش برای گروه های مورد مطالعه به طور مجزا و به طور کلی تأکید نموده اند. چنین موضوعی به دنبال پاسخ به این پرسش است که آیا مدل تدوین شده برای سنجش سازه مورد مطالعه به لحاظ علمی قابل قبول است ؟
اگر مدل تدوین شده فاقد شاخص های برازش قابل قبول است، بررسی برابری پارامترها در بین گروه ها و یا مقایسه میانگین هایی که بر مبنای آن مدل حاصل شده است عملی غیر منطقی است.
بر این مبنا ضرورت دارد تا در وهله اول مشخص شود که آیا داده های گرد آوری شده مدل اندازه گیری تدوین شده را مورد حمایت قرار می دهند یا خیر؟ در صورتی که پاسخ منفی است ضرورت دارد تا با انجام اصلاحات در مدل تدوین شده به مدل قابل قبول تری دست یابیم. مورد حمایت قرار گرفتن مدل نظری تدوین شده برای هر گروه به طور جداگانه نیز ضروری است.
به عبارت دیگر نمی توان به صرف این که مدل اندازه گیری به طور کلی و بدون توجه به گروه های مورد مقایسه از شاخص های برازش مطلوبی برخوردار است، انتظار داشت که امکان مقایسه این مدل در بین دو گروه فراهم باشد.
معادل بودن اندازه گیری در گروه های مورد مطالعه
همانطور که ذکر شد دومین پیش فرض برای آزمون فرضیه های مربوط به برابری میانگین های سازه های پنهان در مدل های عاملی تأییدی برابر بودن مدل اندازه گیری با تأکید بر بارهای عاملی معرف های مختلف تعریف شده برای اندازه گیری سازه پنهان است.
پیش فرض مورد بررسی عنوان می کند که پارامترهای آزاد در مدل اندازه گیری فوق برای دو گروه مردان و زنان یکسان است. به لحاظ روش شناختی چنین فرضی به معنای آن است که ماتریس کواریانس بازسازی شده بر مبنای پارامترهای برآورد شده برای هر یک از دو گروه معادل یکدیگرند و با یکدیگر تفاوت معناداری ندارند. شکل کلی فرضیه صفر برای بررسی برابری پارامترها در مدل یکسان برای نمونه های چندگانه به شکل زیر نوشته می شود :
که در آن نماد ماتریس کواریانس بازتولید شده بر مبنای پارامترهای برآورد شده و G نماد تعداد گروه های مورد مطالعه است.
آزمون چنین فرضیه ای منوط به این است که در وهله اول مقدار آماره کای دو مدل برآورد شود. سپس بارهای عاملی آزاد تعریف شده برای برآورد، برای دو گروه قید برابر بودن زده می شوند. در این مدل مقدار کای دو مدل دارای قیدهای برابری محاسبه می شود. اگر مدل بدون قید برابری پارامترها را مدل 1 و مدل دارای قید برابری را مدل 2 بنامیم آن گاه برای تأیید فرضیه صفری که در واقع پی فرض ماست انتظار داریم که مقدار تفاوت کای دو مدل با درجه آزادی حاصل از تفاضل درجات آزادی دو مدل 1 و 2 ، از مقدار توزیع کای دو در سطح اطمینان 95% کوچکتر باشد.
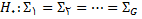


سلام. لطفا سوالات و نظرات خود در خصوص اين مطلب را در همين بخش ديدگاه مطرح نماييد. از طريق ايميل از پاسخ ما مطلع خواهيد شد.
براي جستجو در ميان کامنت ها از Ctrl + f استفاده نماييد.